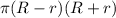Answer:
Look below
Explanation:
(a) The area of the shaded region is the area of the larger rectangle minus the area of the smaller rectangle.
Start by finding the area of the larger rectangle:
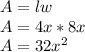
Then, find the area of the smaller rectangle:
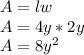
Therefore the area of the shaded region is:
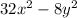
Note that we still need to factor it...
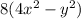
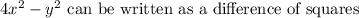
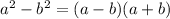
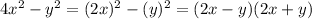
Therefore the fully factored form is:
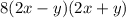
(b) The area of the shaded region is the area of the larger circle minus the area of the smaller circle.
Start by finding the area of the larger circle:
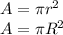
The area of the smaller circle is:
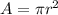
Therefore the difference is:

We can factor out
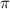
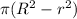
Note this can again be written as a difference of squares:
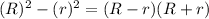
Therefore the fully factored form is: