Explanation:
Let a be the price of 1 adult ticket.
Let c be the price of 1 child ticket.
given,
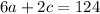
as equation 1,
and
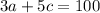
as equation 2.
Now we will solve for a and c using elimination method of simultaneous equations.
Now we multiply equation 2 by 2 to eliminate a and solve for c.
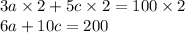
This new equation will be equation 3.
Now we will use equation 1 - equation 3 to eliminate a and solve for c.
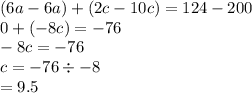
Now substitute c into equation 2.
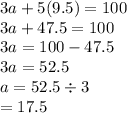
Therefore one adult ticket will cost $17.50 and one child ticket will cost $9.50.