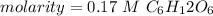Question

What is the molarity of an aqueous solution that contains 78g of C6H12O6 dissolved in 2500 mL of solution?

Answer 1

`\boxed {\boxed {\sf molarity = 0.17 \ M \ C_6H_12O_6}}`

Step-by-step explanation:

Molarity is found by dividing the moles of solute by liters of solution.

`molarity = \frac {moles}{liters}`

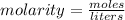
We are given grams of a compound and milliliters of solution, so we must make 2 conversions.

1. Gram to Moles

We must use the molar mass. First, use the Periodic Table to find the molar masses of the individual elements.

• C: 12.011 g/mol
• H: 1.008 g/mol
• O: 15.999 g/mol

Next, look at the formula and note the subscripts. This tells us the number of atoms in 1 molecule. We multiply the molar mass of each element by its subscript.

6(12.011)+12(1.008)+6(15.999)=180.156 g/mol

Use this number as a ratio.

`\frac {180.156 \ g\ C_6H_12 O_6}{ 1 \ mol \ C_6H_12O_6}`

Multiply by the given number of grams.

`78 \ g \ C_6H_12O_6 *\frac {180.156 \ g\ C_6H_12 O_6}{ 1 \ mol \ C_6H_12O_6}`

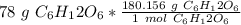
Flip the fraction and divide.

`78 \ g \ C_6H_12O_6 *\frac { 1 \ mol \ C_6H_12O_6}{180.156 \ g\ C_6H_12 O_6}`

`\frac { 78 \ mol \ C_6H_12O_6}{180.156 }= 0.432958102977 \ mol \ C_6H_12O_6`

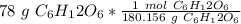
2. Milliliters to Liters

There are 1000 milliliters in 1 liter.

`\frac {1 \ L }{ 1000 \ mL}`

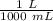
Multiply by 2500 mL.

`2500 \ mL* \frac {1 \ L }{ 1000 \ mL}`

`2500 * \frac {1 \ L }{ 1000 }= 2.5 \ L`

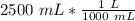
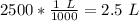
3. Calculate Molarity

Finally, divide the moles by the liters.

`molarity = \frac {0.432958102977 \ mol \ C_6H_12O_6}{ 2.5 \ L}`

`molarity = 0.173183241191 \ mol \ C_6H_12O_6/L`

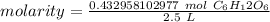
The original measurement has 2 significant figures, so our answer must have the same. That is the hundredth place and the 3 tells us to leave the 7.

`molarity \approx 0.17 \ mol \ C_6H_12O_6 /L`

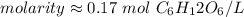
1 mole per liter is also equal to 1 M.

`molarity = 0.17 \ M \ C_6H_12O_6`