Question

write the equation of the line that has the indicated slope and contains the indicated point. express the final equation in standard form. m= 1/2, (6,8)

Answer 1

`x - 2y = -10`

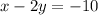
Explanation:

1) Use the point-slope formula
`y-y_1 = m(x-x_1)` to write the equation of the line in point-slope form with the given information. From there, we can convert it to standard form. Substitute values for
`m`,
`x_1`, and
`y_1` in the formula.

Since
`m`, or the slope, is equal to
`(1)/(2)`, substitute
`(1)/(2)` for
`m` in the formula. Since
`x_1` and
`y_1` represent the x and y values of a point the line intersects, substitute the x and y values of (6,8) into the formula as well. This gives the following equation:

`y-8 = (1)/(2) (x-6)`

2) Now, convert the equation above into standard form, represented by the equation
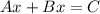`Ax + Bx = C`. Expand the right side, move the terms with the variables to the left side, then move the constants to the right side. Make sure that
`A` isn't negative and all the terms are integers and relatively prime.

`y-8=(1)/(2)(x-6)\\y-8 = (1)/(2) x-3\\-(1)/(2) x+y -8=-3\\-(1)/(2) x+y=5\\x -2y = -10`

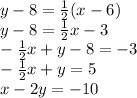
So, the answer is
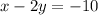`x - 2y = -10`.