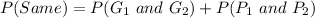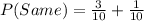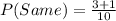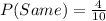Question

Scott and Letitia are brother and sister. After dinner, they have to do the dishes, with one washing and the other drying. They are having trouble deciding who will do what task, so they came up with a method based on probability. Letitia grabs some spoons and puts the is a bag. Some have purple handles and others have green handles. Scott has to pick two of the spoons. If their handles are the same, Scott will wash. If they are different colors, he will dry. It turns out there are two purple spoons and three green ones. What is the probability of Scott washing the dishes?

Answer 1

The probability that Scott will wash is 2.5

Explanation:

Given

Let the events be: P = Purple and G = Green

`P = 2`

`G = 3`

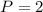
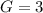
Required

The probability of Scott washing the dishes

If Scott washes the dishes, then it means he picks two spoons of the same color handle.

So, we have to calculate the probability of picking the same handle. i.e.

`P(Same) = P(G_1\ and\ G_2) + P(P_1\ and\ P_2)`

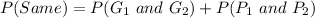
This gives:

`P(G_1\ and\ G_2) = P(G_1) * P(G_2)`

`P(G_1\ and\ G_2) = (n(G))/(Total) * (n(G)-1)/(Total - 1)`

`P(G_1\ and\ G_2) = (3)/(5) * (3-1)/(5- 1)`

`P(G_1\ and\ G_2) = (3)/(5) * (2)/(4)`

`P(G_1\ and\ G_2) = (3)/(10)`

`P(P_1\ and\ P_2) = P(P_1) * P(P_2)`

`P(P_1\ and\ P_2) = (n(P))/(Total) * (n(P)-1)/(Total - 1)`

`P(P_1\ and\ P_2) = (2)/(5) * (2-1)/(5- 1)`

`P(P_1\ and\ P_2) = (2)/(5) * (1)/(4)`

`P(P_1\ and\ P_2) = (1)/(10)`

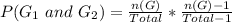
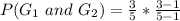
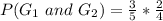
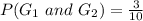
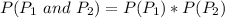
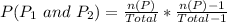
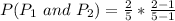
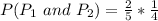
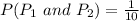
Note that: 1 is subtracted because it is a probability without replacement

So, we have:

`P(Same) = P(G_1\ and\ G_2) + P(P_1\ and\ P_2)`

`P(Same) = (3)/(10) + (1)/(10)`

`P(Same) = (3+1)/(10)`

`P(Same) = (4)/(10)`

`P(Same) = (2)/(5)`