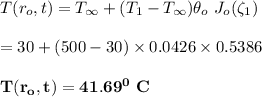Question

As part of a heat treatment process, cylindrical, 304 stainless steel rods of 100-mm diameter are cooled from an initial temperature of 500 C by suspending them in an oil bath at 30 C. If a convection coefficient of 500 W/m2 K is maintained by circulation of the oil, how long does it take for the centerline of a rod to reach a temperature of 50 C, at which point it is withdrawn from the bath

Answer 1

Step-by-step explanation:

Given that:

diameter = 100 mm

initial temperature = 500 ° C

Conventional coefficient = 500 W/m^2 K

length = 1 m

We obtain the following data from the tables A-1;

For the stainless steel of the rod
`\overline T = 548 \ K`

`\rho = 7900 \ kg/m^3`

`K = 19.0 \ W/mk \\ \\ C_p = 545 \ J/kg.K`

`\alpha = 4.40 * 10^(-6) \ m^2/s \\ \\ B_i = (h(\rho/4))/(K) \\ \\ =0.657`

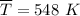
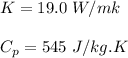
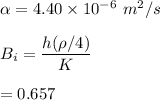
Here, we can't apply the lumped capacitance method, since Bi > 0.1

`\theta_o = (T_o-T_(\infty))/(T_i -T_\infty)} \\ \\ \theta_o = (50-30)/(500 -30)} \\ \\ \theta_o = 0.0426\\`

`0.0426 = c_1 \ exp (- E^2_1 F_o_)\\ \\ \\ 0.0426 = 1.1382 \ exp (-10.9287)^2 \ f_o \\ \\ = f_o = (In(0.0374))/(0.863) \\ \\ f_o = 3.81`

`t_f = (f_o r^2)/(\alpha) \\ \\ t_f = (3.81 * (0.05)^2)/(4.40 * 10^(-6)) \\ \\ t_f= 2162.5 \\ \\ t_f = 36 mins`

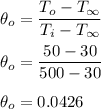
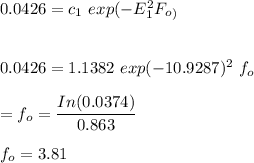
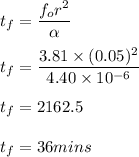
However, on a single rod, the energy extracted is:

`\theta = pcv (T_i - T_(\infty) )(1 - (2 \theta)/(c) J_1 (\zeta) ) \\ \\ = 7900 \\times 546 * 0.007854 * (500 -300) (1 - (2 * 0.0426)/(1.3643)) \\ \\ \theta = 1.54 * 10^7 \ J`

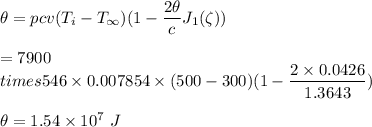
Hence, for centerline temperature at 50 °C;

The surface temperature is:

`T(r_o,t) = T_(\infty) +(T_1 -T_(\infty)) \theta_o \ J_o(\zeta_1) \\ \\ = 30 + (500-30) * 0.0426 * 0.5386 \\ \\ \mathbf{T(r_o,t) = 41.69 ^0 \ C}`