Question

What is the vertex of the quadratic function below?

y = x2 - 8x+1
A. (4, -15)
B. (8, 1)
C. (-8, 129)
D. (-4, 15)

Answer 1

A. (4, -15)

Explanation:

`\underline{\mathrm{Parabola\:equation\:in\:polynomial\:form}}`

`\mathrm{The\:vertex\:of\:an\:up-down\:facing\:parabola\:of\:the\:form}\:y=ax^2+bx+c\:\mathrm{is}\:x_v=-(b)/(2a)`

`\mathrm{The\:parabola\:params\:are:}`

`a=1,\:b=-8,\:c=1`

`x_v=-(b)/(2a)`

`x_v=-(\left(-8\right))/(2\cdot \:1)`

`x_v=4`

`\mathrm{Plug\:in}\:x_v=4\:\mathrm{to\:find\:the}\:y_v\mathrm{value}`

`y_v=-15`

`\mathrm{Therefore\:the\:parabola\:vertex\:is}`

`\left(4,\:-15\right)`

`\mathrm{If}\:a<0,\:\mathrm{then\:the\:vertex\:is\:a\:maximum\:value}`

`\mathrm{If}\:a>0,\:\mathrm{then\:the\:vertex\:is\:a\:minimum\:value}`

`a=1`

`\mathrm{Vertex\:of}\:x^2-8x+1:\quad \mathrm{Minimum}\space\left(4,\:-15\right)`

Answer 2

Option A: (4, -15).

Explanation:

Given the quadratic function, y = x² - 8x + 1, where a = 1, b = -8, and c = 1:

Solve for the x-coordinate of the vertex:

We can use the following equation to solve for the x-coordinate of the vertex:

`\displaystyle\mathsf{x\:=\:(-b)/(2a)}`

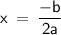
Substitute the given values into the formula:

`\displaystyle\mathsf{x\:=\:(-b)/(2a)\:=\:(-(-8))/(2(1))\:=\:(8)/(2)\:=\:4}`

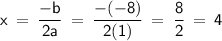
Hence, the x-coordinate of the vertex is 4.

Solve for the y-coordinate of the vertex:

Next, substitute the x-coordinate of the vertex into the given quadratic function to solve for its corresponding y-coordinate:

y = x² - 8x + 1

y = (4)² - 8(4) + 1

y = 16 - 32 + 1

y = -15

Therefore, the vertex of the given quadratic function, y = x² - 8x + 1, is: x = 4, y = -15, or (4, -15). Thus, the correct answer is Option A: (4, -15).