Question

A cylindrical specimen of this alloy 12 mm in diameter and 188 mm long is to be pulled in tension. Assume a value of 0.34 for Poisson's ratio.Calculate the stress (in MPa) necessary to cause a 0.0105 mm reduction in diameter.

Answer 1

This question is incomplete, the missing image in uploaded along this answer below.

Answer:

The required stress is 200 Mpa

Step-by-step explanation:

Given the data in the question;

diameter D = 12 mm = 12 × 10⁻³ m

Length L = 188 mm = 188 × 10⁻³ m

Poisson's ratio v = 0.34

Reduction in diameter Δd = 0.0105 mm = 0.0105 × 10⁻³ m

The transverse strain will;

εˣ = Δd / D

εˣ = -0.0105 × 10⁻³ / 12 × 10⁻³ m

εˣ = -0.00088

The longitudinal strain will be;

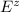`E^z` = - ( εˣ / v )

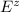`E^z` = - ( -0.00088 / 0.34 )

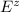`E^z` = - ( - 0.002588 )

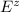`E^z` = 0.0026

Now, Using the values for strain, we get the value of stress from the graph provided in the question, ( first image uploaded below.

From the graph, in the Second image;

The stress is 200 Mpa

Therefore, The required stress is 200 Mpa