Question

Two ball bearings from different manufacturers are being considered for a certain application. Bearing A has a catalog rating of 2.12 kN based on a catalog rating system of 3000 hours at 500 rev/min. Bearing B has a catalog rating of 7.5 kN based on a catalog that rates at 106 cycles. For a given application, determine which bearing can carry the larger load.

Answer 1

F
`_D` for A > F
`_D` for B

Hence, Bearing A can carry the larger load

Step-by-step explanation:

Given the data in the question,

First lets consider an application which requires desired speed of n₀ and a desired life of L₀.

Lets start with Bearing A

so we write the relation between desired load and life catalog load and life;

`F_R(L_Rn_R60)^(1/a)` =
`F_D(L_Dn_D60)^(1/a)`

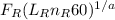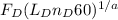
where F
`_R` is the catalog rating( 2.12 kN)

L
`_R` is the rating life ( 3000 hours )

n
`_R` is the rating speed ( 500 rev/min )

F
`_D` is the desired load

L
`_D` is the desired life ( L₀ )

n
`_D` is the the desired speed ( n₀ )

Now as we know, a = 3 for ball bearings

so we substitute

`2.12( 3000 * 500 * 60 )^{1/3` =
`F_D( L_0n_060)^{1/3`

950.0578 =
`F_D( L_0n_0)^(1/3) 3.914867`

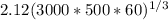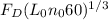
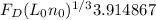
950.0578 / 3.914867 =
`F_D( L_0n_0)^(1/3)`

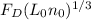
242.6794 =
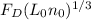
`F_D( L_0n_0)^(1/3)`

F
`_D` for A = (242.6794 /
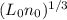`( L_0n_0)^(1/3)` ) kN

Therefore the load that bearing A can carry is (242.6794 /
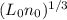`( L_0n_0)^(1/3)` ) kN

Next is Bearing B

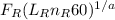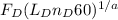
`F_R(L_Rn_R60)^(1/a)` =
`F_D(L_Dn_D60)^(1/a)`

F
`_R` = 7.5 kN,
`(L_Rn_R60) = 10^6`

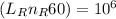
Also, for ball bearings, a = 3

so we substitute

`7.5(10^6)^{1/3` =
`F_D(L_0n_060)^(1/3)`

750 =
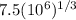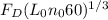
`F_D(L_0n_0)^(1/3) 3.914867`

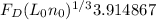
750 / 3.914867 =
`F_D(L_0n_0)^(1/3)`

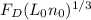
191.5773 =
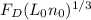
`F_D(L_0n_0)^(1/3)`

F
`_D` for B = ( 191.5773 /
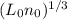`(L_0n_0)^(1/3)` ) kN

Therefore, the load that bearing B can carry is ( 191.5773 /
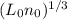`(L_0n_0)^(1/3)` ) kN

Now, comparing the Two results above,

we can say;

F
`_D` for A > F
`_D` for B

Hence, Bearing A can carry the larger load