Answer:
the highest rate of heat transfer allowed is 0.9306 kW
Step-by-step explanation:
Given the data in the question;
Volume = 4L = 0.004 m³
V
 = V
= V
 = 0.002 m³
= 0.002 m³
Using Table ( saturated water - pressure table);
at pressure p = 175 kPa;
v
 = 0.001057 m³/kg
= 0.001057 m³/kg
v
 = 1.0037 m³/kg
= 1.0037 m³/kg
u
 = 486.82 kJ/kg
= 486.82 kJ/kg
u
 2524.5 kJ/kg
2524.5 kJ/kg
h
 = 2700.2 kJ/kg
= 2700.2 kJ/kg
So the initial mass of the water;
m₁ = V
 /v
/v
 + V
+ V
 /v
/v

we substitute
m₁ = 0.002/0.001057 + 0.002/1.0037
m₁ = 1.89414 kg
Now, the final mass will be;
m₂ = V/v

m₂ = 0.004 / 1.0037
m₂ = 0.003985 kg
Now, mass leaving the pressure cooker is;
m
 = m₁ - m₂
= m₁ - m₂
m
 = 1.89414 - 0.003985
= 1.89414 - 0.003985
m
 = 1.890155 kg
= 1.890155 kg
so, Initial internal energy will be;
U₁ = m
 u
u
 + m
+ m
 u
u

U₁ = (V
 /v
/v
 )u
)u
 + (V
+ (V
 /v
/v
 )u
)u

we substitute
U₁ = (0.002/0.001057)(486.82) + (0.002/1.0037)(2524.5)
U₁ = 921.135288 + 5.030387
U₁ = 926.165675 kJ
Now, using Energy balance;
E
 - E
- E
 = ΔE
= ΔE
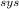
QΔt - m
 h
h
 = m₂u₂ - U₁
= m₂u₂ - U₁
QΔt - m
 h
h
 = m₂u
= m₂u
 - U₁
- U₁
given that time = 75 min = 75 × 60s = 4500 sec
so we substitute
Q(4500) - ( 1.890155 × 2700.2 ) = ( 0.003985 × 2524.5 ) - 926.165675
Q(4500) - 5103.7965 = 10.06013 - 926.165675
Q(4500) = 10.06013 - 926.165675 + 5103.7965
Q(4500) = 4187.690955
Q = 4187.690955 / 4500
Q = 0.9306 kW
Therefore, the highest rate of heat transfer allowed is 0.9306 kW