Answer:
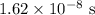
Step-by-step explanation:
 = Vacuum permittivity =
= Vacuum permittivity =
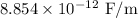
 = Area =
= Area =

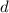 = Distance between plates = 1 mm
= Distance between plates = 1 mm
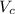 = Changed voltage = 60 V
= Changed voltage = 60 V
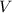 = Initial voltage = 100 V
= Initial voltage = 100 V
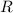 = Resistance =
= Resistance =
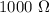
Capacitance is given by

We have the relation
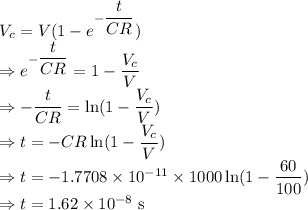
The time taken for the potential difference to reach the required level is
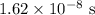 .
.