Answer:
a) 0.39984 = 39.984% probability of no orders in five minutes.
b) 0.06563 = 6.563% probability of 3 or more orders in five minutes.
c) The length of time is 0.63 hours
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
Orders arrive at a Web site according to a Poisson process with a mean of 11 per hour.
This means that
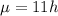 , in which h is the number of hours.
, in which h is the number of hours.
a) Probability of no orders in five minutes.
Five minutes means that
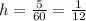 , so
, so
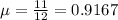
This probability is P(X = 0). So

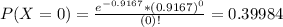
0.39984 = 39.984% probability of no orders in five minutes.
b) Probability of 3 or more orders in five minutes.
This is:
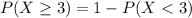
In which

So

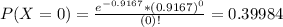

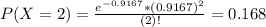
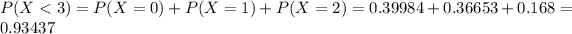

0.06563 = 6.563% probability of 3 or more orders in five minutes.
c) Length of a time interval such that the probability of no orders in an interval of this length is 0.001.
This is h for which:
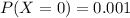
We have that:

And
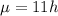
So
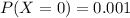
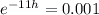


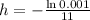
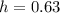
The length of time is 0.63 hours