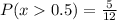Answer:
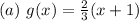
![(b)\ h(y) = (1)/(3)[1 + 4y]](https://img.qammunity.org/2022/formulas/mathematics/college/e7n977whgw798kkty6pfnd5b2m4vkoe7dn.png)

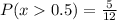
Explanation:
Given
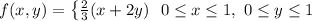
Solving (a): The marginal density of X
This is calculated as:
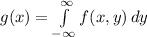
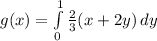
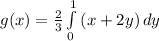
Integrate
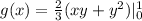
Substitute 1 and 0 for y
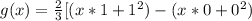
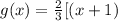
Solving (b): The marginal density of Y
This is calculated as:


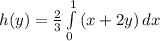
Integrate
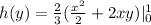
Substitute 1 and 0 for x
![h(y) = (2)/(3)[((1^2)/(2) + 2y*1) - ((0^2)/(2) + 2y*0) ]](https://img.qammunity.org/2022/formulas/mathematics/college/14zxml07l37td19yoxanvp6dogjpjjbihg.png)
![h(y) = (2)/(3)[((1)/(2) + 2y)]](https://img.qammunity.org/2022/formulas/mathematics/college/46j53ma903y7cqed5wk2vkq0dpnybf4xtr.png)
![h(y) = (1)/(3)[1 + 4y]](https://img.qammunity.org/2022/formulas/mathematics/college/dq4ajwl1809l4xdlx0ors35jruuv2k6jxi.png)
Solving (c): The probability that the drive-through facility is busy less than one-half of the time.
This is represented as:
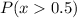
The solution is as follows:
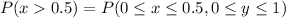
Represent as an integral

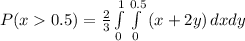
Integrate w.r.t. x
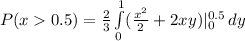
![P(x>0.5) =(2)/(3)\int\limits^1_0 [((0.5^2)/(2) + 2*0.5y) -((0^2)/(2) + 2*0y)], dy](https://img.qammunity.org/2022/formulas/mathematics/college/1yeu8l865x8x3hem2p77dmhctvfbs5gkt2.png)
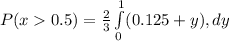
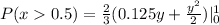
![P(x>0.5) =(2)/(3)[(0.125*1 + (1^2)/(2)) - (0.125*0 + (0^2)/(2))]](https://img.qammunity.org/2022/formulas/mathematics/college/5ids3mx98qa52knr5ks53o02b3me0q3k9u.png)
![P(x>0.5) =(2)/(3)[(0.125 + (1)/(2))]](https://img.qammunity.org/2022/formulas/mathematics/college/5fc5n0i7h5099p9aactfnimoolxp9o0dmn.png)
![P(x>0.5) =(2)/(3)[(0.125 + 0.5]](https://img.qammunity.org/2022/formulas/mathematics/college/zsl98hc0ms1iqjf5nluwd7wjmjkizlxjfv.png)
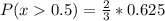
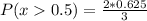
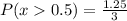
Express as a fraction, properly