Question

Please help and show workings!

Answer 1

`\displaystyle E)\: 162 √(3)`

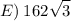
Explanation:

we are given a side a polygon

and said to figure out the area

recall the formula of regular polygon

`\displaystyle \: \frac{ {na}^(2) }{4} \cot \left( \frac{ {180}^( \circ) }{n} \right)`

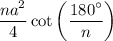
where a represents the length of a side

and n represents the number of sides

the given shape has 6 sides

and has a length of
`\displaystyle 6√(3)`

so our n is 6 and a is 6√3

substitute the value of n and a:

`\displaystyle \: \frac{ {6 \cdot \:( 6 √(3) })^(2) }{4} \cot \left( \frac{ {180}^( \circ) }{6} \right)`

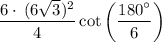
reduce fraction:

`\displaystyle \: \frac{ {6 \cdot \:( 6 √(3) })^(2) }{4} \cot \left( \frac{ { \cancel{180}^( \circ)} ^{ {30}^( \circ) } }{ \cancel{6 \: } } \right)`

`\displaystyle \: \frac{6 \cdot \: (6 \sqrt{ {3} } {)}^(2) }{4} \cot( {30}^( \circ) )`

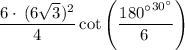
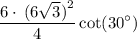
simplify square:

`\displaystyle \: (6 \cdot \: 36 \cdot \: 3 )/(4) \cot( {30}^( \circ) )`

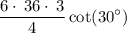
reduce fraction:

`\displaystyle \: \frac{6 \cdot \: \cancel{36} \: ^(9) \cdot \: 3 }{ \cancel{ 4 \: } } \cot( {30}^( \circ) )`

`\displaystyle \: 6 \cdot \: 9 \cdot \: 3 \cot( {30}^( \circ) )`

simplify multiplication:

`\displaystyle \: 162\cot( {30}^( \circ) )`

recall unit circle:

`\displaystyle \: 162 √(3)`

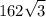
hence, our answer is E

Answer 2

`162√(3)`

Explanation:

The equation for finding the area of a hexagon with a side length is

`(s^23√(3) )/2`

insert
`6√(3)`

and you are left with 162\sqrt{3}

Hope that helps :)