Answer:
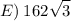
Explanation:
we are given a side a polygon
and said to figure out the area
recall the formula of regular polygon
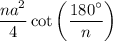
where a represents the length of a side
and n represents the number of sides
the given shape has 6 sides
and has a length of
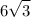
so our n is 6 and a is 6√3
substitute the value of n and a:
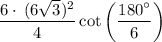
reduce fraction:
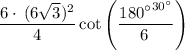
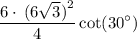
simplify square:
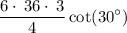
reduce fraction:
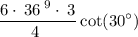
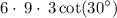
simplify multiplication:
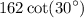
recall unit circle:
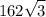
hence, our answer is E