Explanation:
By Pythagoras' Theorem,
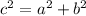
where c is always the largest number.
a and b can be interchangeable between the 2nd largest and the 3rd largest numbers.
Given a = 8, b = 15 and c = 17,
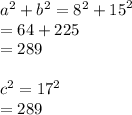
Since c^2 = a^2 + b^2 , 8 , 15 and 17 are pythagorean triplets.
Now let's move on to 9, 40 and 41.
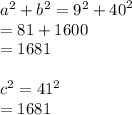
Since c^2 = a^2 + b^2 , 9 , 40 and 41 are pythagorean triplets.
Last let's move on to 4,7 and 8.
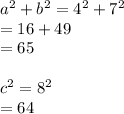
Since a^2+b^2 IS NOT EQUAL to c^2, 4,7 and 8 ARE NOT pythagorean triplets.