Given:
The expression is

To find:
The expression which is not a correct way to rewrite the given expression.
Solution:
We have,

Using distributive property, we get
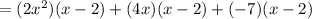

Using distributive property the given expression can rewritten as:

Only the expression in option A is not a correct way to rewrite the given expression because
 is not distributed to
is not distributed to
 properly.
properly.
Therefore, the correct option is A.