Answer:
(-infinity, -32/81] U (0, positive infintiy).
( use the sideways 8 symbol for infinity).
Explanation:
The range is all possible y values in a function.
We can find the inverse of the function to find the range.
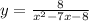
Replace x with y
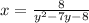
Write the LCD as two binomial,
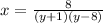
Multiply both sides by both binomial
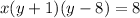
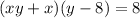
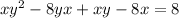
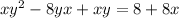
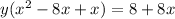
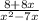
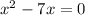
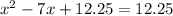
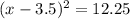
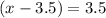

Plug that in to the function to find it range.
We get approximately
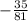
So this means a point on our function must include -35/81.
The vertical asymptote is 0 so our y cannot be zero but it goes infinitely up so our range is
(-infinity, -32/81]U (0, positive infintiy).
( use the sideways 8 symbol for infinity).