Question

How do I find the range of this rational function, how do I do the steps in order to find it, please help!!!​

Answer 1

Range= (0,∞) and (-∞,0)

Explanation:

Theres no real process to finding this out you just look at what type of function you have, your graph and your asymptote. We can see that the parts above the asymptote go up and towards ∞ and the part below goes down to -∞ but they can not cross 0

Answer 2

(-infinity, -32/81] U (0, positive infintiy).

( use the sideways 8 symbol for infinity).

Explanation:

The range is all possible y values in a function.

We can find the inverse of the function to find the range.

`y = \frac{8}{ {x}^(2) - 7x - 8 }`

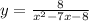
Replace x with y

`x = \frac{8}{ {y}^(2) - 7y - 8 }`

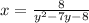
Write the LCD as two binomial,

`x = (8)/((y + 1)(y - 8))`

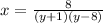
Multiply both sides by both binomial

`x(y + 1)(y - 8) = 8`

`(xy + x)(y - 8) = 8`

`x {y}^(2) - 8yx + xy - 8x = 8`

`xy {}^(2) - 8yx + xy = 8 + 8x`

`y( {x}^(2) - 8x + x) = 8 + 8x`

`\frac{8 + 8x}{ {x}^(2) - 7x }`

`{x}^(2) - 7x = 0`

`{x}^(2) - 7x + 12.25 = 12.25`

`(x - 3.5) {}^(2) = 12.25`

`(x - 3.5) = 3.5`

`x = 3.5`

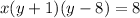
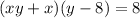
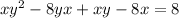
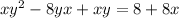
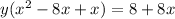
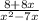
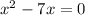
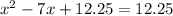
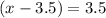
Plug that in to the function to find it range.

We get approximately

`- (35)/(81)`

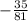
So this means a point on our function must include -35/81.

The vertical asymptote is 0 so our y cannot be zero but it goes infinitely up so our range is

(-infinity, -32/81]U (0, positive infintiy).

( use the sideways 8 symbol for infinity).