Answer:
Explanation:
13). Area of a square = (Side)²
= (BC)²
Since, diagonals of a square bisect each other at 90°,
ΔBOC is a right triangle.
By applying Pythagoras theorem in the given triangle,
BC² = OB² + OC²
BC² = 2(OB)²
BC² = 2(7√2)²
BC =
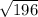
Area of square ABCD = (BC)²
= (√196)²
= 196 units²
14). Measure of interior angles of the regular hexagon = 120°
Area of the regular hexagon =
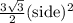
From the given picture,
m∠BAC = m∠ABC = m∠ACB = 60°
Therefore, ΔABC is an isosceles triangle.
And all sides of this triangle will be equal in measure.
AB = AC = BC = 9 units
Area of the given regular hexagon =
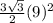
= 210.44 square units
≈ 210.4 square units