Answer:
a) f(g(x)) =
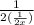 =
=
 = x
= x
g(f(x)) =
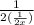 =
=
 = x
= x
f and g are inverses
b) f(g(x)) = x + 3 + 3 = x + 6
g(f(x)) = x + 3 + 3 = x + 6
f and g are not inverses
Explanation:
a)
f(g(x)) =
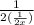 =
=
 = x
= x
g(f(x)) =
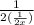 =
=
 = x
= x
Since f(g(x)) = g(f(x)) = x, then f and g are inverses
b)
f(g(x)) = x + 3 + 3 = x + 6
g(f(x)) = x + 3 + 3 = x + 6
Since f(g(x)) = g(f(x)) ≠ x, then f and g are not inverses