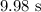Answer:
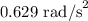 counterclockwise
counterclockwise
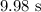
Step-by-step explanation:
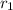 = Small drive wheel radius = 2.2 cm
= Small drive wheel radius = 2.2 cm
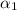 = Angular acceleration of the small drive wheel =
= Angular acceleration of the small drive wheel =
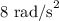
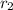 = Radius of pottery wheel = 28 cm
= Radius of pottery wheel = 28 cm
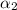 = Angular acceleration of pottery wheel
= Angular acceleration of pottery wheel
As the linear acceleration of the system is conserved we have
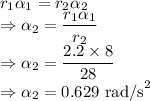
The angular acceleration of the pottery wheel is
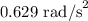 .
.
The rubber drive wheel is rotating in clockwise direction so the pottery wheel will rotate counterclockwise.
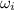 = Initial angular velocity = 0
= Initial angular velocity = 0
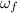 = Final angular velocity =
= Final angular velocity =
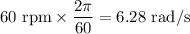
t = Time taken
From the kinematic equations of linear motion we have
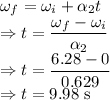
The time it takes the pottery wheel to reach the required speed is