Answer:
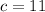
Explanation:
Given
Let the three sides be a, b and c
Such that:
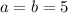
Required
Find c such that a, b and c do not form a triangle
To do this, we make use of the following triangle inequality theorem
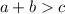
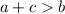

To get a valid triangle, the above inequalities must be true.
To get an invalid triangle, at least one must not be true.
Substitute:
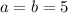

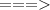
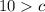
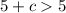
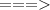
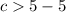
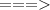
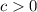
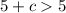
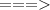
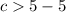
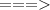
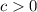
The results of the inequality is:
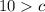 and
and
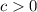
Rewrite as:
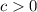 and
and
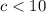

This means that, the values of c that make a valid triangle are 1 to 9 (inclusive)
Any value outside this range, cannot form a triangle
So, we can say:
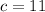 , since no options are given
, since no options are given