Question

Help me please I need to turn it in before midnight...

Answer 1

The statement which explains how the total time spent in the air is affected as the projectile's angle of launch increases from 25 degrees to 50 degrees is;

C. Increasing the angle from 25° to 50° will increase the total time spent in the air

Step-by-step explanation:

The equation that can be used to find the total time, T, spent in the air of a projectile is given as follows;

`T = (2 \cdot u \cdot sin(\theta) )/(g)`

Where;

T = The time of flight of the projectile = The time spent in the air

u = The initial velocity of the projectile

θ = The angle of launch of the projectile

g = The acceleration due to gravity ≈ 9.81 m/s²

Given that sin(50°) > sin(25°), when the angle of launch, θ, is increased from 25 degrees to 50 degrees, we have;

Let T₁ represent the time spent in the air when the angle of launch is 25°, and let T₂ represent the time spent in the air when the angle of launch is 50°, we have;

`T_1 = (2 \cdot u \cdot sin(25^(\circ)) )/(g)`

`T_2 = (2 \cdot u \cdot sin(50^(\circ)) )/(g)`

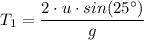
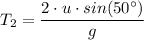
sin(50°) > sin(25°), therefore, we have;

`(2 \cdot u \cdot sin(50^(\circ)) )/(g) > (2 \cdot u \cdot sin(25^(\circ)) )/(g)`

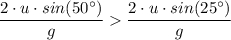
Therefore;

T₂ > T₁

Therefore, increasing the angle at which the projectile is launched from 25° to 50° will increase the total time spent in the air.