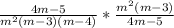Answer:

Explanation:
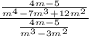
Factor the equation:
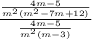
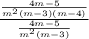
Rewrite to suit the format of multiplying two fractions. Remember, dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second. A reciprocal of a fraction is when one switches the place of the numerator and the denominator, that is, the value on top (numerator), and the value on the bottom (denominator).
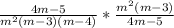
Simplify, take out common terms that are found on both the numerator and denominator