Answer:
10.3 %
Skills needed: Markup
Explanation:
1) There is a formula for mark-up that allows one to directly solve for the percentage, and it will be broken down below.
---> Markup is the percent increase for a product or service.
---> It finds out how much percent a product has increased in price from the original price.
---> There are certain markup percentages used by stores to determine the price of a new product or a product very high in demand.
2) The formula mark-up, which is the percent raise in the product price is as shown below:
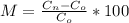
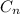 is the new (usually increased) cost
is the new (usually increased) cost
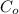 is the original cost
is the original cost
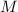 is markup (as a %)
is markup (as a %)
(The 100 is there to convert the decimal answer into a percent).
3) We can use this for this problem, as the original price (Which is last year's price) is 145, and the new price is 160:
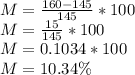
(Note: I rounded 15 divided by 145 to the nearest ten-thousandths place as that is the amount of decimal places needed).
10.34% rounds to 10.3% when rounded to the nearest tenth (as stated).