Answer:
the temperature of the intermediate reservoir is 624.5 K
Step-by-step explanation:
Given the data in the question
The two Carnot heat engines are operating in series;
[ T
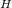 ]
]
↓
((1)) ⇒ W

↓
[ T
 ]
]
↓
((2)) ⇒ W

[ T
 ]
]
The maximum possible efficiency for any heat engine is the Carnot efficiency;
η
 = 1 -
= 1 -
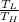
the thermal efficiencies if both engines are the same will be;
η
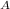 = η
= η
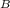
1 -
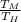 = 1 -
= 1 -
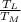
1 - 1 -
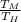 = -
= -
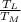
-
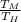 = -
= -
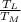
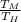 =
=
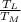
T
 ² = T
² = T
 × T
× T
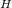
T
 = √(T
= √(T
 × T
× T
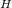 )
)
source temperature of the first engine T
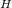 = 1300 K
= 1300 K
sink temperature of the second engine T
 = 300 K
= 300 K
we substitute
T
 = √(300 × 1300)
= √(300 × 1300)
T
 = √390000
= √390000
T
 = 624.4998 K ≈ 624.5 K
= 624.4998 K ≈ 624.5 K
Therefore, the temperature of the intermediate reservoir is 624.5 K