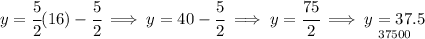Question

Pls help i screenshotted my question

Answer 1

1)

to get the equation of any straight line, we simply need two points off of it, let's use those two points on the picture below to the left side.

`(\stackrel{x_1}{3}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{9}~,~\stackrel{y_2}{20}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{20}-\stackrel{y1}{5}}}{\underset{run} {\underset{x_2}{9}-\underset{x_1}{3}}}\implies \cfrac{15}{6}\implies \cfrac{5}{2}`

`\begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{5}=\stackrel{m}{\cfrac{5}{2}}(x-\stackrel{x_1}{3}) \\\\\\ y-5=\cfrac{5}{2}x-\cfrac{15}{2}\implies y=\cfrac{5}{2}x-\cfrac{15}{2}+5\implies y=\cfrac{5}{2}x-\cfrac{5}{2}`

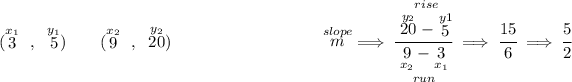
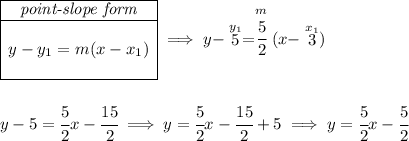
now, the line that closely models it is 2.5x, as you can see in the picture below at the right side.

2)

now, we'll be using the equation that we got for the best fit line.

what is "y" when x = 16?

`y=\cfrac{5}{2}(16)-\cfrac{5}{2}\implies y=40-\cfrac{5}{2}\implies y=\cfrac{75}{2}\implies \underset{37500}{y=37.5}`