Answer:
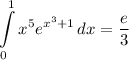
General Formulas and Concepts:
Symbols
- e (Euler's number) ≈ 2.71828
Algebra I
- Exponential Rule [Multiplying]:
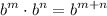
Calculus
Differentiation
- Derivatives
- Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Integration
- Integrals
- Definite Integrals
- Integration Constant C
Integration Rule [Reverse Power Rule]:
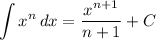
Integration Rule [Fundamental Theorem of Calculus 1]:
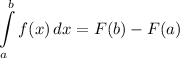
Integration Property [Multiplied Constant]:
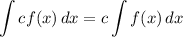
U-Substitution
Integration by Parts:
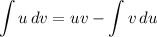
- [IBP] LIPET: Logs, inverses, Polynomials, Exponentials, Trig
Explanation:
Step 1: Define
Identify
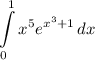
Step 2: Integrate Pt. 1
- [Integrand] Rewrite [Exponential Rule - Multiplying]:
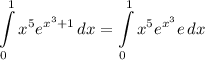
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
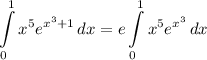
Step 3: Integrate Pt. 2
Identify variables for u-solve.
- Set u:
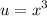
- [u] Differentiate [Basic Power Rule]:
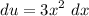
- [u] Rewrite:
![\displaystyle x = \sqrt[3]{u}](https://img.qammunity.org/2022/formulas/mathematics/college/fzouqddmnij8fhwp452pcllfzvadtdfx01.png)
- [du] Rewrite:
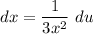
Step 4: Integrate Pt. 3
- [Integral] U-Solve:
![\displaystyle \int\limits^1_0 {x^5e^(x^3 + 1)} \, dx = e\int\limits^1_0 {x^5e^{(\sqrt[3]{u})^3}(1)/(3x^2)} \, du](https://img.qammunity.org/2022/formulas/mathematics/college/g6z228b5ao4zoxgxmxijw2f8jqh1robo19.png)
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
![\displaystyle \int\limits^1_0 {x^5e^(x^3 + 1)} \, dx = (e)/(3)\int\limits^1_0 {x^5e^{(\sqrt[3]{u})^3}(1)/(x^2)} \, du](https://img.qammunity.org/2022/formulas/mathematics/college/v4g3zmm0gexgzp12mvuof3anbgm9ia2r9i.png)
- [Integral] Simplify:
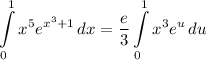
- [Integrand] U-Solve:
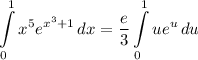
Step 5: integrate Pt. 4
Identify variables for integration by parts using LIPET.
- Set u:

- [u] Differentiate [Basic Power Rule]:
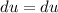
- Set dv:
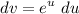
- [dv] Exponential Integration:
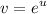
Step 6: Integrate Pt. 5
- [Integral] Integration by Parts:
![\displaystyle \int\limits^1_0 {x^5e^(x^3 + 1)} \, dx = (e)/(3) \bigg[ ue^u \bigg| \limits^1_0 - \int\limits^1_0 {e^u} \, du \bigg]](https://img.qammunity.org/2022/formulas/mathematics/college/s27lkkys44yqxkvrfab2ntxgdqh0zhkivw.png)
- [Integral] Exponential Integration:
![\displaystyle \int\limits^1_0 {x^5e^(x^3 + 1)} \, dx = (e)/(3) \bigg[ ue^u \bigg| \limits^1_0 - e^u \bigg| \limits^1_0 \bigg]](https://img.qammunity.org/2022/formulas/mathematics/college/wv7gplf2drh2v0au2ns3y7c092ducb109n.png)
- Evaluate [Integration Rule - Fundamental Theorem of Calculus 1]:
![\displaystyle \int\limits^1_0 {x^5e^(x^3 + 1)} \, dx = (e)/(3)[ e - e ]](https://img.qammunity.org/2022/formulas/mathematics/college/96z9mkjidh5bxobjq5aa9rdn6efjgq5ly4.png)
- Simplify:
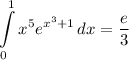
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration
Book: College Calculus 10e