Answer:
a) the torque required is 10.53 N-m
b) The magnitude force applied tangentially is 12.33 N
Step-by-step explanation:
Given the data in the question;
mass m = 1.765 kg
radius r = 0.854 m
first we calculate the moment of inertia;
 =
=
 mr²
mr²
we substitute
 =
=
 × 1.765 × (0.854)²
× 1.765 × (0.854)²
 = 0.514897 kg.m²
= 0.514897 kg.m²
a)
Find the torque required to bring the sphere from rest to an angular velocity of 317 rad/s, clockwise, in 15.5 s
ω
 = 0
= 0
ω
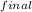 = 317 rad/s
= 317 rad/s
t = 15.5 s
we know that; ω
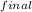 = ω
= ω
 + ∝t
+ ∝t
so we substitute
317 = 0 + ∝(15.5)
∝ = 317 / 15.5
∝ = 20.4514 rad/s²
so
ζ =
 × ∝
× ∝
we substitute
ζ = 0.514897 × 20.4514
ζ = 10.53 N-m
Therefore, the torque required is 10.53 N-m
b)
What magnitude force applied tangentially at the equator would provide the needed torque.
ζ = F × r
we substitute
10.53 = F × 0.854
F = 10.53 / 0.854
F = 12.33 N
Therefore, magnitude force applied tangentially is 12.33 N