Question

The area of a sector of a circle of radius 5

cm, formed by an arc of length 3.5 cm is
(a) 8 cm?
(b) 8.75 cm?
(c) 9.5 cm?
(d) 7.9 cm?
​

Answer 1

Answer: (b)

Explanation:

Given

the radius of circle r=5 cm

arc length
`l=3.5\ cm`

Arc length is also given by

`l=(\theta )/(360^(\circ))* 2\pi r`

`\Rightarrow 3.5=(\theta )/(360^(\circ))* 2\pi * 5\\\\\Rightarrow \theta =40.10^(\circ)`

Area of the sector is given by

`\Rightarrow A=(\theta )/(360^(\circ))* \pi r^2\\\\\Rightarrow A=(40.101^(\circ))/(360^(\circ))* 3.142* 5^2\\\\\Rightarrow A=8.749\approx 8.75\ cm^2`

Answer 2

A = 8.75 cm²

Explanation:

Given that,

Radius, r = 5 cm

The arc length, l = 3.5 cm

We need to find the area of a sector. Let
`\theta` be the angle. So,

`\theta=(l)/(r)\\\\\theta=(3.5)/(5)\\\\\theta=0.7\ rad`

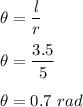
The formula for the area of sector when
`\theta` is in radian is given by :

`A=(1)/(2)* \theta r^2\\\\A=(1)/(2)* 0.7* 5^2\\\\A=8.75\ cm^2`

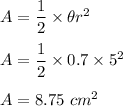
So, the area of the sector is 8.75 cm².