Question

Find y, ST and TU
Please help!

Answer 1

Given:

`ST=4y,TU=2y+6`

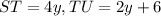
To find:

The value of y, ST and TU.

Solution:

In triangle STV and UTV,

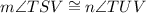`m\angle TSV\cong n\angle TUV` (Given right angles)

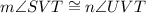`m\angle SVT\cong n\angle UVT` (Given)

`TV\cong TV` (Common side)

The corresponding two angles and a non included sides in both triangles are congruent. So, the triangles are congruent by using AAS congruence postulate.

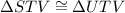`\Delta STV\cong \Delta UTV` (AAS congruence postulate)

Corresponding parts of congruent triangles are congruent. So,

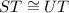`ST\cong UT` (CPCTC)

`4y=2y+6`

`4y-2y=6`

`2y=6`

`y=3`

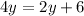
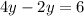
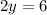
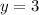
Now,

`ST=4y`

`ST=4(3)`

`ST=12`

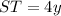
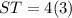
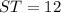
And,

`TU=2y+6`

`TU=2(3)+6`

`TU=6+6`

`TU=12`

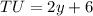
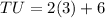
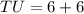
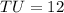
Therefore,
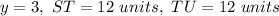`y=3,\ ST=12\ units,\ TU=12\ units`.