Given:
The system of equations is:
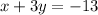
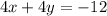
To find:
The solution for the given system of equations.
Solution:
We have,
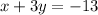 ..(i)
..(i)
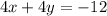 ...(ii)
...(ii)
Multiply equation (i) by 4, to make common coefficient of x.
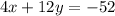 ..(iii)
..(iii)
Subtract (ii) from (iii).
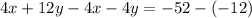
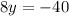
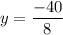
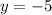
Putting
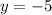 in (i), we get
in (i), we get
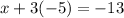
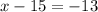
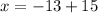
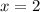
Therefore, the solution of the given system of equations is
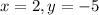 .
.