I'll do #1 & #2, but you have to do the rest on your own, I'm sorry.
#1 Answer:
The median height of giraffes is:
18 feet.
Step-by-step explanation:
We are given height, in feet, of 9 giraffes as:
18, 16, 22, 14, 17, 19, 15 ,19,22
Now to find the median height of giraffes in the zoo we need to arrange the given data set in ascending order as:
14 15 16 17 18 19 19 22 22
Now we know that median is the central tendency of the data i..e it lie in the middle of the data set.
The value that lie in the middle of the given data set is:
18.
Hence, the median height of giraffes is:
18 feet.
#2 Answer:
The median of the sizes of the four parks is:
Option: C 33 acres.
Step-by-step explanation:
We are given area of four parks as:
27 acres 30 acres 34 acres 49 acres.
We know that the median of a data is the central tendency of a data and always lie in between or middle of the data set.
Hence, here the median will lie between 30 and 34
and hence is calculated as:
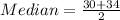
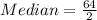

which is close to 33.
Hence, the median size of the park is:
33 acres.