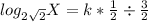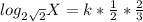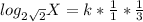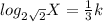Question

The logarithm of a number to the base V2 is k. What is its logarithm to the base 2v2 ?​

Answer 1

`log_(2\sqrt 2) X = (1)/(3)k`

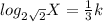
Explanation:

Given

Let the number be X

From the first statement, we have:

`log_(\sqrt 2) X = k`

Required

Find
`log_(2\sqrt 2) X`

`log_(\sqrt 2) X = k`

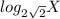
using the following law of logarithm

`log_ab = n, b=a^n`

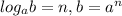
So:

`log_(\sqrt 2) X = k`

`X = √(2)^k`

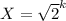
Substitute:
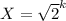`X = √(2)^k` in
`log_(2\sqrt 2) X`

`log_(2\sqrt 2) X = log_(2\sqrt 2) ( √(2)^k)`

`log_(2\sqrt 2) X = klog_(2\sqrt 2) √(2)`

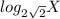
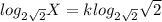
Apply the following law:

`log_ab = (log\ b)/(log\ a)`

`log_(2\sqrt 2) X = k\frac{log\ \sqrt 2}{log\ {2\sqrt 2}}`

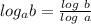
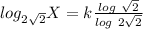
Express the square roots as power

`log_(2\sqrt 2) X = k\frac{log\ 2^(1)/(2)}{log\ {2 * 2^(1)/(2)}}`

`log_(2\sqrt 2) X = k\frac{log\ 2^(1)/(2)}{log\ {2^(3)/(2)}}`

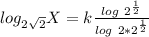
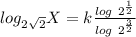
using the following law of logarithm

`log_ab = n, b=a^n`

`log_(2\sqrt 2) X = k((1)/(2)log\ 2)/((3)/(2)log\ 2)}`

`log_(2\sqrt 2) X = k((1)/(2))/((3)/(2))}`

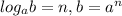
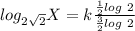
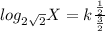
Rewrite as:

`log_(2\sqrt 2) X = k * (1)/(2) /(3)/(2)`

`log_(2\sqrt 2) X = k * (1)/(2) *(2)/(3)`

`log_(2\sqrt 2) X = k * (1)/(1) *(1)/(3)`

`log_(2\sqrt 2) X = (1)/(3)k`