Question

Two jugs are similar. The smaller jug has radius 4cm and the bigger jug has radius

6cm and surface area 125cm2. The smaller jug has a volume of 400cm.
Calculate
the area of the smaller jug.

Answer 1

Given:

Two jugs are similar. The smaller jug has radius 4 cm and the bigger jug has radius 6 cm and surface area 125 cm².

To find:

The area of the smaller jug.

Solution:

If two figures are similar, then the ratio of their areas is proportional to the square of the corresponding sides of the figures.

Two jugs are similar. So,

`\frac{\text{Area of smaller jug}}{\text{Area of bigger jug}}=\frac{(\text{Radius of smaller jug})^2}{(\text{Radius of bigger jug})^2}`

`\frac{\text{Area of smaller jug}}{125}=((4)^2)/((6)^2)`

`\frac{\text{Area of smaller jug}}{125}=(16)/(36)`

`\text{Area of smaller jug}=(4)/(9)* 125`

`\text{Area of smaller jug}\approx 55.56`

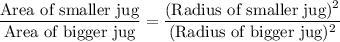
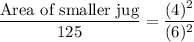
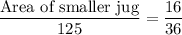
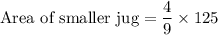
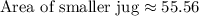
Therefore, the area of the smaller jug is about 55.56 cm².