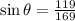The ratio
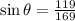 is accurate for the described tower and guy-wire configuration.
is accurate for the described tower and guy-wire configuration.
Let's denote the angle between the tower and the guy wire as θ. The length of the guy wire is the hypotenuse of a right triangle formed by the tower, the ground, and the guy wire.
According to trigonometry, the sine of an angle in a right triangle is defined as the ratio of the opposite side to the hypotenuse. In this case, the opposite side is the height of the tower at point B (119 feet), and the hypotenuse is the length of the guy wire.
Therefore, the sine of angle θ (sin θ) is given by:
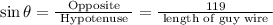
Now, we need to find the length of the guy wire. This can be determined using the Pythagorean Theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b):
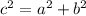
In this case, a is the height of the tower at point B (119 feet), b is the distance from point A to the base of the tower (120 feet), and c is the length of the guy wire.
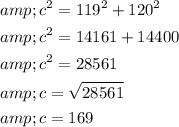
Now that we have the length of the guy wire (169 feet), we can substitute it back into the original expression for sin θ:
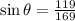
Therefore, the correct answer is: C)