Answer:
173,949 lb
Explanation:
Volume of a sphere:
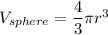
A hemisphere is half of a sphere, so its volume is half of the volume of a sphere with the same diameter. Also, radius = diameter/2.
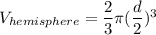
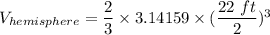
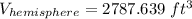
Now we use the density of water to find the weight of the water contained in the tank.
weight = volume * density
weight = 2787.639 ft^3 * 62.4 lb/ft^3
weight = 173,949 lb