Answer:
d = 4
Explanation:
Given f varies inversely as d² then the equation relating them is
f =
 ← k is the constant of variation
← k is the constant of variation
To find k use the condition when d = 2, f = 6 , then
6 =
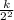 =
=
 ( multiply both sides by 4 )
( multiply both sides by 4 )
24 = k
f =
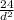 ← equation of variation
← equation of variation
When f = 1.5 , then
1.5 =
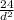 ( multiply both sides by d² )
( multiply both sides by d² )
1.5d² = 24 ( divide both sides by 1.5 )
d² = 16 ( take the square root of both sides )
d =
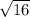 = 4
= 4