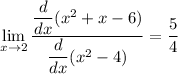Question

Help please

simplify the following using L'Hôpital's Rule:

`\displaystyle\lim_(x\to 2)(x^2+x-6)/(x^2-4)`

`\text{note:explanation is a must}`​

Answer 1

`\displaystyle \: (5)/(4)`

Explanation:

we are given a expression

we are said to solve it using L'Hôpital's Rule

recall, L'Hôpital's Rule:

`\displaystyle \lim _(x \to \: c)( (f(x))/(g(x)) ) = \lim _(x \to \: c) \frac{f ^(')(x) }{ {g}^(')(x) }`

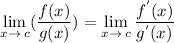
it is to say the ' means derivative

our given expression:

`\displaystyle\lim_( x\to 2)(x^2+x-6)/(x^2-4)`

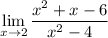
let's apply L'Hôpital's Rule

`\displaystyle\lim_( x\to 2)( (d)/(dx) (x^2+x-6))/( (d)/(dx) (x^2-4))`

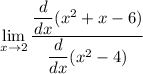
some formulas of derivative

`\displaystyle \: (d)/(dx) {x}^(n) = {nx}^(n - 1)`

`\displaystyle \: (d)/(dx) {x}^{} = 1`

`\displaystyle \: (d)/(dx) {c}^{} = 0`

`\sf \displaystyle \: (d)/(dx) {f}^{} (x) + {g}^{}(x) = {f}^(') (x) + {g}^(')(x)`

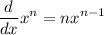
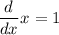
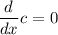
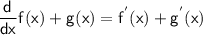
use sum derivative formula to simplify:

`\displaystyle\lim_( x\to 2)( (d)/(dx) (x^2)+ (d)/(dx) (x) + (d)/(dx)( -6))/( (d)/(dx) (x^2) + (d)/(dx) (-4))`

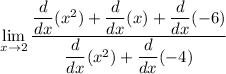
simplify using exponents using exponent derivative formula:

`\displaystyle\lim_( x\to 2)( 2x+ (d)/(dx) (x) + (d)/(dx)( -6))/( 2x + (d)/(dx) (-4))`

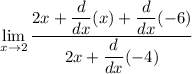
use variable derivative formula to simplify variable:

`\displaystyle\lim_( x\to 2)( 2x+ 1+ (d)/(dx)( -6))/( 2x + (d)/(dx) (-4))`

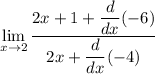
use constant derivative formula to simplify derivative:

`\displaystyle\lim_( x\to 2)( 2x+ 1+ 0)/( 2x + 0)`

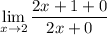
simplify addition:

`\displaystyle\lim_( x\to 2)( 2x+ 1)/( 2x )`

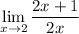
since we are approaching x to 2

we can substitute 2 for x

`\displaystyle\lim_( x\to 2)( 2.2+ 1)/( 2.2 )`

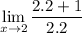
simplify multiplication:

`\displaystyle( 4+ 1)/( 4)`

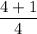
simplify addition:

`\displaystyle \: (5)/(4)`

hence,

`\displaystyle\lim_( x\to 2)( (d)/(dx) (x^2+x-6))/( (d)/(dx) (x^2-4)) = (5)/(4)`

Answer 2

5/4 is your answer hope it helps