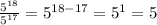Answer:
Supongo que queremos simplificar la expresión dada.
Acá tenemos que recordar las dos relaciones:
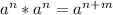
y
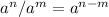
También es útil recordar que:
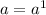
Entonces podemos simplificar nuestra expresión que es:
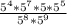
Si usamos la primera relación tanto en el numerador como en el denominador, obtenemos:
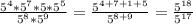
Ahora podemos aplicar la segunda relación: