Given:
Consider the below figure attached with this ques.
To find:
The length of the line segment XZ.
Solution:
According to the tangent-secant theorem, the square of tangent is equal to the product of secant and external segment of secant.
Using tangent-secant theorem, we get
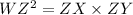
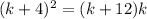
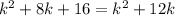
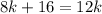
Subtract both sides by 8k.
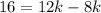
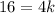
Divide both sides by 4.
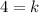
Now,
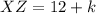
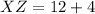
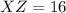
Therefore, the measure of XZ is 16 units.