Question

g 1) The rate of growth of a certain type of plant is described by a logistic differential equation. Botanists have estimated the maximum theoretical height of such plants to be 30 in. At the beginning of an experiment, the height of a plant was 5 in. a) Find an expression for the height of the plant after t days. (To find k, suppose the plant grew to 12 in. after 20 days.) b) What was the height of the plant after 30 days

Answer 1

a) The expression for the height, 'H', of the plant after 't' day is;

`H = \frac{30}{1 + 5\cdot e^{-(2.02732554 * 10^(-3)) \cdot t}}`

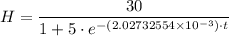
b) The height of the plant after 30 days is approximately 19.426 inches

Explanation:

The given maximum theoretical height of the plant = 30 in.

The height of the plant at the beginning of the experiment = 5 in.

a) The logistic differential equation can be written as follows;

`(dH)/(dt) = K \cdot H \cdot \left( M - {P} \right)`

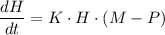
Using the solution for the logistic differential equation, we get;

`H = (M)/(1 + A\cdot e^(-(M\cdot k) \cdot t))`

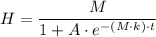
Where;

A = The condition of height at the beginning of the experiment

M = The maximum height = 30 in.

Therefore, we get;

`5 = (30)/(1 + A\cdot e^(-(30\cdot k) \cdot 0))`

`1 + A = (30)/(5) = 6`

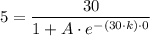
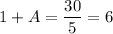
A = 5

When t = 20, H = 12

We get;

`12 = (30)/(1 + 5\cdot e^(-(30\cdot k) \cdot 20))`

`1 + 5\cdot e^(-(30\cdot k) \cdot 20) = (30)/(12) = 2.5`

`5\cdot e^(-(30\cdot k) \cdot 20) = 2.5 - 1 = 1.5`

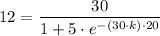
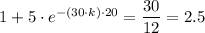
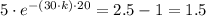
∴ -(30·k)·20 = ㏑(1.5)

k = ㏑(1.5)/(30 × 20) ≈ 6·7577518 × 10⁻⁴

k ≈ 6·7577518 × 10⁻⁴

Therefore, the expression for the height, 'H', of the plant after 't' day is given as follows

`H = \frac{30}{1 + 5\cdot e^{-(30* 6.7577518 * 10^(-4)) \cdot t}} = \frac{30}{1 + 5\cdot e^{-(2.02732554 * 10^(-3)) \cdot t}}`

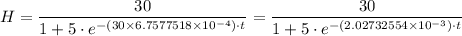
b) The height of the plant after 30 days is given as follows

`H = \frac{30}{1 + 5\cdot e^{-(2.02732554 * 10^(-3)) \cdot t}}`

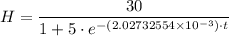
At t = 30, we have;

`H = \frac{30}{1 + 5\cdot e^{-(2.02732554 * 10^(-3)) * 30}} \approx 19.4258866473`

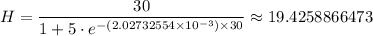
The height of the plant after 30 days, H ≈ 19.426 in.