Answer:
a) The expression for the height, 'H', of the plant after 't' day is;
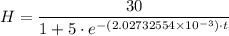
b) The height of the plant after 30 days is approximately 19.426 inches
Explanation:
The given maximum theoretical height of the plant = 30 in.
The height of the plant at the beginning of the experiment = 5 in.
a) The logistic differential equation can be written as follows;
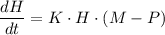
Using the solution for the logistic differential equation, we get;
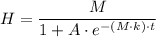
Where;
A = The condition of height at the beginning of the experiment
M = The maximum height = 30 in.
Therefore, we get;
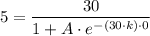
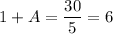
A = 5
When t = 20, H = 12
We get;
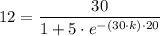
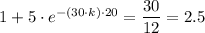
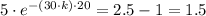
∴ -(30·k)·20 = ㏑(1.5)
k = ㏑(1.5)/(30 × 20) ≈ 6·7577518 × 10⁻⁴
k ≈ 6·7577518 × 10⁻⁴
Therefore, the expression for the height, 'H', of the plant after 't' day is given as follows
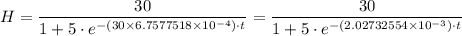
b) The height of the plant after 30 days is given as follows
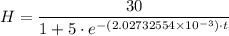
At t = 30, we have;
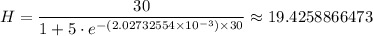
The height of the plant after 30 days, H ≈ 19.426 in.