Question

A trailer truck with a 2000 [kg] cab and a 8000 [kg] trailer is traveling on a level road at 90 [km/hr].The brakes on the trailer fail, and the anti-skid system of the cab provides the largest possible forcewhich will not cause the wheels of the cab to slide. Knowing that the coefficient of static friction isμs= 0.65, determine (a) the shortest time for the rig to come to a stop, (b) the force in the couplingduring that time.

Answer 1

a) t = 19.6 s, b) fr = 1.274 10⁴ N

Step-by-step explanation:

This is a Newton's second law problem

Y Axis

for the cabin

N₁-W₁ = 0

N₁ = W₁

for the trailer

N₂- W₂ = 0

N₂ = W₂

X axis

for the cabin plus trailer, where friction is only in the cabin

fr = (m₁ + m₂) a

the friction force equation is

fr = μ N

we substitute

μ N₁ = (m₁ + m₂) a

μ m₁ g = (m₁ + m₂) a

a = μ g
`(m_1)/(m_1 + m_2)`

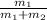
let's calculate

a = 0.65 9.8
`(2000)/(2000+8000)`

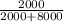
a = 1,274 m / s²

a) to find the stopping distance we can use kinematics

Let's slow down the sI system

v₀ = 90 km / h (1000 m / 1km) (1h / 3600s) = 25 m / s

v = v₀ - a t

when it is stopped its speed is zero

0 = v₀ - at

t = v₀ / a

t = 25 / 1.274

t = 19.6 s

b) the friction force is

fr = 0.65 2000 9.8

fr = 1.274 10⁴ N

This is the braking force and also the forces that couple the cars.