Answer:
a. The thermal efficiency of the actual cycle is 45%
ii) The rate at which energy is rejected by heat transfer to the cold reservoir is 0.55 MW
b. The (maximum) cycle efficiency, is 50%
The rate of energy rejection to the cold reservoir by heat transfer is 0.55 MW
Therefore, there is an increased efficiency and reduced heat rejection in the reversible power cycle working between the given two reservoirs
Step-by-step explanation:
The given parameters are;
The temperature of the hot reservoir,
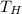 = 600 K
= 600 K
The temperature of the hot reservoir,
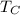 = 300 K
= 300 K
The power output,
 = 0.45 MW = The cycle work per second
= 0.45 MW = The cycle work per second
The heat input from the hot reservoir,
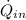 = 1 MW
= 1 MW
a. The thermal efficiency of the actual cycle is given by the work done divided by the heat supplied as follows;
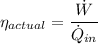
Therefore, we have;
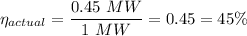
The thermal efficiency of the actual cycle,
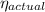 = 45%
= 45%
ii) The rate at which energy is rejected by heat transfer to the cold reservoir,
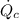 , is given as follows;
, is given as follows;
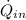 =
=
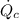 +
+

∴
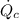 =
=
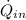 -
-

Therefore, we have;
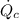 = 1 MW - 0.45 MW = 0.55 MW
= 1 MW - 0.45 MW = 0.55 MW
The rate at which energy is rejected by heat transfer to the cold reservoir,
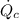 = 0.55 MW
= 0.55 MW
b. For a reversible power cycle, we have the maximum cycle efficiency,
 , given as follows;
, given as follows;


The maximum cycle efficiency,
 = 50%
= 50%
The rate of work done by the cycle,
 , is therefore give as follows;
, is therefore give as follows;
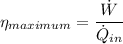
Therefore;
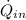 ×
×
 =
=

1 MW × 50% = 0.5 MW =

 = 0.5 MW
= 0.5 MW
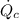 =
=
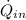 -
-

∴
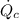 = 1 MW - 0.5MW = 0.5MW
= 1 MW - 0.5MW = 0.5MW
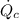 = 0.5MW
= 0.5MW
The rate of energy rejection to the cold reservoir by heat transfer,
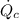 = 0.55 MW
= 0.55 MW
Therefore the frequency and the rate at which energy is rejected by heat transfer to the cold reservoir are both higher for the reversible power cycle