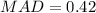Answer:
See below
Explanation:
class-1:
we are given some data 3,4,5,5,5,5,5,5,5,5,6,7
we want to figure out the MAD (Mean absolute deviation) of the given database
remember that,
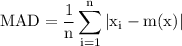
where m(X) represents the mean of the given database and
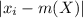 tells us to subtract every data with the got mean and n represents the number of data
tells us to subtract every data with the got mean and n represents the number of data
let figure out m(X)
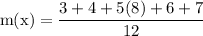
simplify multiplication:
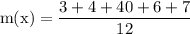
simplify addition:
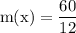
simplify substraction:
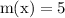
let's figure out
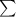 and
and

![\displaystyle\begin{array} \hline |x_(i) - m(x) | & \displaystyle\sum_(i = 1) ^(n) |x_(i) - m(x) | \\ \hline |3 - 5 | & 2 \\ \hline | 4 - 5 | &1 \\ \hline |5(8) - 5(8)| &0 \\ \hline |6 - 5|&1 \\ \hline |7 - 5| &2 \\ \hline \\ \text{total} & 5 \\ \hline\end{array}]()
last part let's figure out MAD
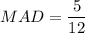
simplify division:
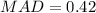
Class-2:
likewise class-2
given database 7,8,9,9,9,9,9,9,9,9,10,11
figure out m(X)
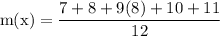
simplify multiplication:
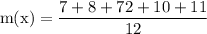
simplify addition:
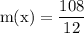
simplify division:
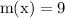
likewise
figure out
 and
and

![\displaystyle\begin{array} \hline |x_(i) - m(x) | & \displaystyle\sum_(i = 1) ^(n) |x_(i) - m(x) | \\ \hline |7 - 9 | & 2 \\ \hline | 8- 9 | &1 \\ \hline |9(8) - 9(8)| &0 \\ \hline |10 - 9|&1 \\ \hline |11- 9| &2 \\ \hline \\ \text{total} & 5 \\ \hline\end{array}]()
figure out MAD
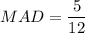
simplify division: