The hypotenuse is approximately 91.31 units.
The length of the hypotenuse of the triangle can be found using the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the two legs is equal to the square of the hypotenuse.
In this case, the legs of the triangle are AB and BC, and the hypotenuse is AC.
Given that AB = (6x+4) and BC = 5x, we can substitute the value of x and solve:
AB = (6(11)+4) = 70
BC = 5(11) = 55
AC = √(
 ) = √(
) = √(
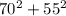 ) ≈ 91.31 (rounded to the nearest tenth)
) ≈ 91.31 (rounded to the nearest tenth)