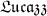Question

Exponential Functions

Solve the Equation

A) -3
B) 1
C) 4 and half
D) 3

Answer 1

• C) 4 and a half

Explanation:

To solve this question, we can use either of the 2 below given methods:

1. Rule of exponents
2. Logarithms

1. Rule of Exponents:

`2 ^ { 7-2x } = ( 1 )/( 4 )\\\rightarrow 2 ^ { 7-2x } = ( 1 )/( 2^(2) )`

Now, by using the law →
`x^(-y) = (1)/(x^(y))`...

`2 ^ { 7-2x } = ( 1 )/( 2^(2) )\\2 ^ { 7-2x } = 2^(-2)`

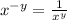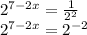
Now, let's take the exponential values as the base values are equal.

`7 - 2x = - 2\\- 2x = - 2 + (-7)\\- 2x = - 9\\\boxed{x = (9)/(2) = 4.5}`

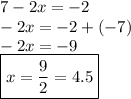
2. Logarithms:

`2 ^ { 7-2x } = ( 1 )/( 4 )\\\rightarrow2^(-2x+7)=(1)/(4)`

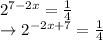
Now, take the logarithm of both the sides of the equation.

`\log(2^(-2x+7))=\log((1)/(4))`

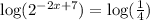
We know that, the logarithm of a number raised to an exponential power is power times the logarithm of the number. So,

`\log(2^(-2x+7))=\log((1)/(4)) \\ \rightarrow \left(-2x+7\right)\log(2)=\log((1)/(4))`

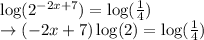
Now, divide both the sides of the equstion by log (2).

`-2x+7=(\log((1)/(4)))/(\log(2))`

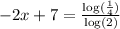
According to the change of base formula,
`(\log(x))/(\log(y))` =
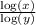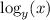`\log_(y)(x)`. Then,

`-2x+7=\log_(2)\left((1)/(4)\right)`

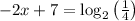
By subtracting 7 from both the sides of the equation & then simplifing it further....

`-2x=-2-7 \\-2x = - 9\\\boxed{x = (9)/(2) = 4.5}`

• We get the same value by using either of the 2 methods.
• The value of x = 9/2 or 4.5

_____________

Hope it helps!

`\mathfrak{Lucazz}`

Answer 2

option c .

Explanation:

Given exponential equation is ,

`\longrightarrow 2^(7-2x)= (1)/(4)`

As we know that 4 = 2² , so ;

`\longrightarrow 2^(7-2x)= (1)/(2^2)`

Recall that ,
`a^(-m)=(1)/(a^m)` .So ;

`\longrightarrow 2^(7-2x)= 2^(-2)`

Since the bases are equal we can compare the powers as ,

`\longrightarrow 7-2x = -2`

Subtracting 7 on both sides,

`\longrightarrow -2x = -9`

Divide both sides by -2,

`\longrightarrow x =(-9)/(-2)`

Simplify,

`\longrightarrow \underline{\underline{ x = 4.5 }}`

Hence the correct option is C .