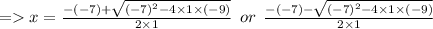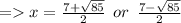Question

X² - 7x = 9

solve the following equations by using the quadratic formula.Leave your answer in surd form
​

Answer 1

x=7+ the square root of 85 /2 , x = 7- the square root of 85/2

Step-by-step explanation: hope I helped

Answer 2

`x = (7 + √(85) )/(2) \:\: or \:\: (7 - √(85) )/(2)`

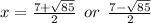
Explanation:

__________________________________________________________

FACTS TO KNOW BEFORE SOLVING :-

Quadratic Formula :-

For a quadratic equation ax² + bx + c = 0 , by using quadratic formula the roots of the equation are :-

`x = \frac{-b + {√(b^2 - 4ac) } }{2a} \:\: or \:\: (-b - √(b^2 - 4ac) )/(2a)`

__________________________________________________________

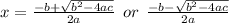
Lets solve the equation x² - 7x - 9 = 0 by quadratic formula.

`=> x = (-(-7) + √((-7)^2 - 4 * 1 * (-9)) )/(2 * 1) \:\: or \:\: (-(-7) - √((-7)^2 - 4 * 1 * (-9)) )/(2 * 1)`

`=> x = (7 + √(85) )/(2) \:\: or \:\: (7 - √(85) )/(2)`